The paper (Sundararajan, Taly et al. 2017) identifies two axioms – sensitivity and implementation invariance that attribution methods ought to satisfy. Based on the axioms, the authors designed a new attribution method called integrated gradients. The method requires no modification to the original model and needs only a few calls to the standard gradient operator.

Notations

Symbol	Meaning
	a function that maps
	inputs
	baseline input

Two Axioms

They found that other feature attribution methods in literature break at least one of the two axioms, including DeepLift, LRP, deconvolutional networks and guided backpropagation. In fact, the paper points out that methods based on gradients of the output with respect to inputs (backpropagation) and without a referencing baseline break the axiom of sensitivity.

Idea 1: the axiom of sensitivity (a)

For every input and baseline that differ in one feature but have different predictions then the differing feature should be given a non-zero attribution.

Idea 1a: gradients violate sensitivity

Because of gradient saturation. The lack of sensitivity causes gradients to focus on irrelevant features. An example from Hung-yi Lee’s tutorial:

Long noses are important features for elephants. Within a certain range (say 0.5 m to 1 m), the longer the nose, the more likely the animal is an elephant

However, when the length of noses is greater than 1 m, the marginal contribution of this feature becomes close to none, and other features become more salient.

Idea 2: the axiom of implementation invariance

Two networks are functionally equivalent if their outputs are equal for all inputs, despite having very different implementations. Intuitively if the two networks are functionally equivalent, the results of attribution methods should be identical.

Idea 2a: the chain rule for gradients is essentially about implementation invariance

where and can be thought of as the input and output of a system, and being some implementation detail of the system. The gradient of output to can be computed either directly by , ignoring the intermediate function or by invoking the chain rule via .

Idea 2b: methods with discrete gradients break the axiom of implementation invariance

Methods like LRP and DeepLift break this axiom because the chain rule does not hold for discrete gradients in general.

Therefore, these methods fail to satisfy implementation invariance.

Integrated Gradients (IG)

Idea 3: the formulation of integrated gradients

They consider a straight-line path in from the baseline to the input and compute the gradients at all points along the path. Integrated gradients are obtained by cumulating these gradients.

The integrated gradient along the ith dimension for an input and baseline is defined as follows. Here, is the gradient of along the ith dimension.

$∷$

Comment: the equation is equivalent to

Idea 4: IG satisfies an axiom called completeness

The axiom of completeness: the attributions add up to the difference between the output of at the input and the baseline . IG satisfies the axiom of sensitivity because Completeness implies Sensitivity(a) and is thus a strengthening of the Sensitivity axiom. This is because Sensitivity refers to a case where the baseline and the input differ only in one variable, for which Completeness asserts that the difference in the two output values is equal to the attribution to this variable.

If is differentiable almost everywhere, then

Intuition: even though is a high-dimensional function, is a line (or path). The difference in the elevation of the function is the net effect (i.e., sum) of each feature’s marginal contribution to the total change of elevation. Therefore, it is the sum of integrations rather than performing integration sequentially.

Mathematically speaking, applying gradient theorem to line integral:

For more discussion please refer to (Lerma and Lucas 2021).

If there is a baseline near zero (), then there is an interpretation of the resulting attributions that ignores the baseline and amounts to the distribution of the output to the individual input features.

The Uniqueness of IG

Idea 5: perturbation can be unnatural

Perturbation can be unnatural. Therefore, the drop in the evaluation metric is coupled by feature importance and artifacts i.e., sampling from a new data distribution, especially where feature interactions exist and are important.

Authors found out that every empirical evaluation technique they could think of could not differentiate between artifacts that stem from perturbing the data, a misbehaving model, and a misbehaving attribution method. This observation supports the axiomatic approach in designing a good attribution method.

Idea 6: the definition of path methods

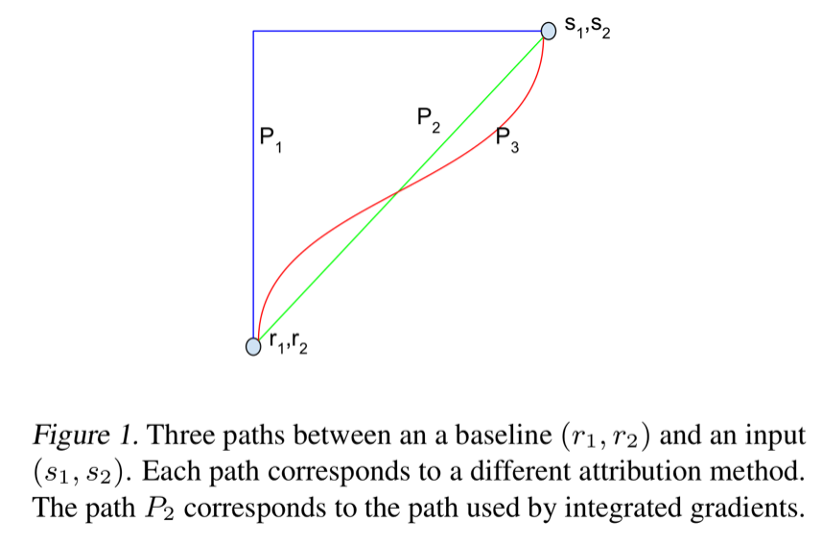Image source: (Sundararajan, Taly et al. 2017)

Attribution methods based on path integrated gradients are collectively known as path methods.

Let be a smooth function specifying a path in from the baseline to the input , i.e.,and .

Formally:

where is the gradient of along the ith dimension at .

Notice that integrated gradients is a path method for the straight-line path specified

Idea 6a: all path methods satisfy Implementation Invariance

This is from the fact that they are defined using the underlying gradients, which do not depend on the implementation. As pointed out in Idea 2a, the chain rule is essentially about implementation invariance.

Idea 6b: all path methods satisfy completeness

As discussed previously, if is differentiable almost everywhere, then

Idea 6c: all path methods satisfy Sensitivity (a)

As established previously, completeness implies sensitivity (a). All path methods satisfy completeness, therefore, sensitivity (a) as well.

Idea 7: path methods are the only methods to satisfy certain desirable axioms

Idea 7a: the axiom of Sensitivity (b) (Friedman 2004)

Also called the axiom of dummy. If the function implemented by the deep work does not depend mathematically on some variable, then the attribution to that variable is always zero.

Idea 7b: the axiom of linearity

Suppose that we linearly composed two deep networks modeled by the functions functions and form a third network that models the function , then the weighted sum of the attributions for and with weights and respectively. Intuitively, we would like the attributions to preserve any linearity within the network.

Idea 7c: Path methods are the only attribution methods that always satisfy Implementation Invariance, Sensitivity (b), Linearity, and Completeness. (Friedman 2004)

Integrated gradients correspond to a cost-sharing method called Aumann-Shapley. This argument is proven in Theorem 1 of (Friedman 2004).

Idea 8: Integrated gradient is the unique path method that is symmetry-preserving

Idea 8a: the definition of symmetry-preserving

Symmetry-preserving: and are symmetric w.r.t. if and only if for all values of and .

It is natural to ask for symmetry-preserving attribution methods because if two variables play the same role in the network (i.e., they are symmetric and have the same values in the baseline and the input) then they ought to receive the same attribution.

Idea 8b: Proof of the theorem that integrated gradient is the unique path method that is symmetry-preserving

Please refer to (Sundararajan, Taly et al. 2017) for simple proof and (Lerma and Lucas 2021) for more rigorous proof.

Integrated Gradients Approximation

where is the number of steps in the Riemann approximation of the integral. The default approximation method in Captum is Gauss-Legendre quadrature. Gauss-Legendre quadrature is a deterministic integral approximation routine based on discretizing the integral.

The integral of over the interval is approximated by the weighted sum of terms. Gauss-Legendre quadrature determines both the sampling points and their corresponding weights.

References

Friedman, E. J. (2004). "Paths and consistency in additive cost sharing." International Journal of Game Theory 32(4): 501-518.
Lerma, M. and M. Lucas (2021). "Symmetry-Preserving Paths in Integrated Gradients." arXiv preprint arXiv:2103.13533.
Sundararajan, M., et al. (2017). Axiomatic attribution for deep networks. International Conference on Machine Learning, PMLR.